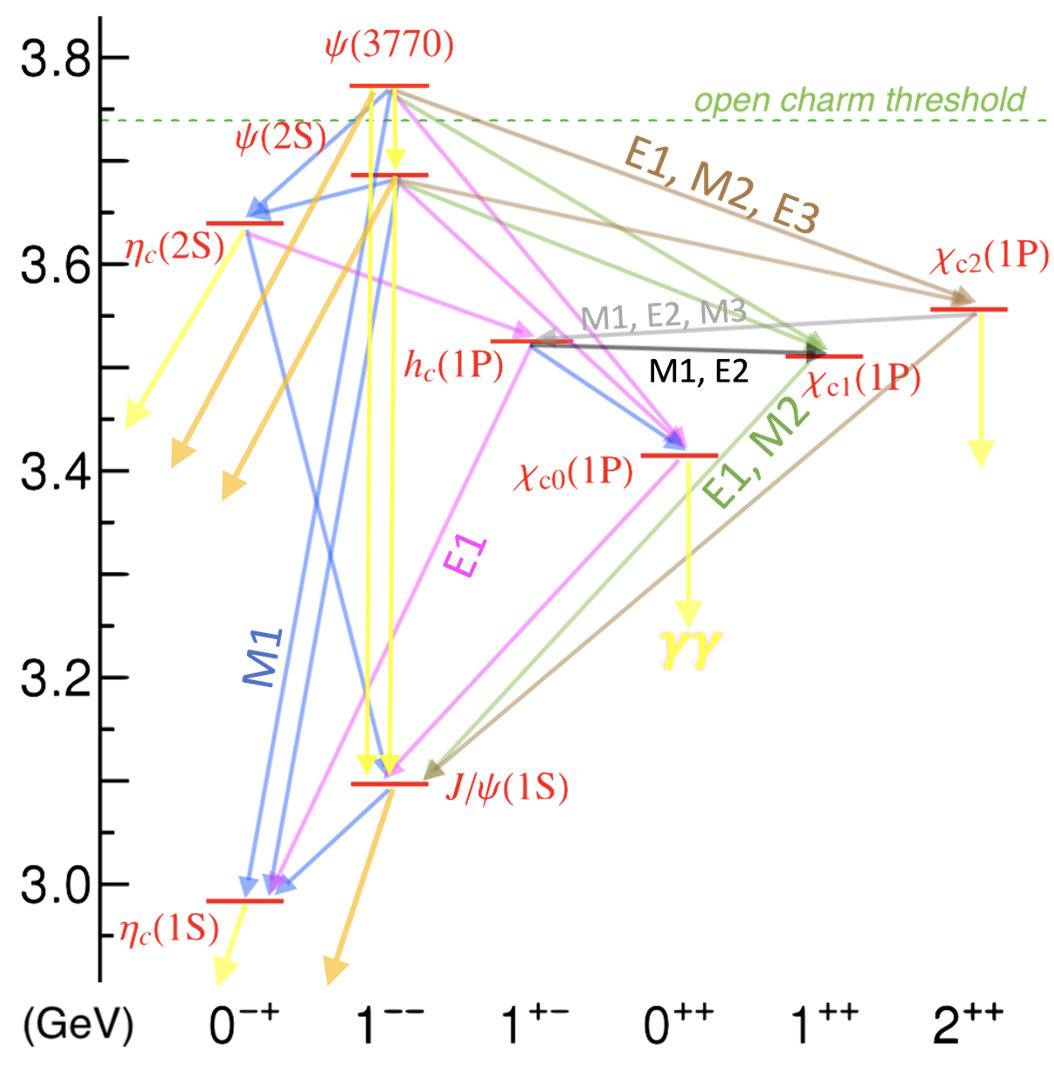
我最近的工作主要在高能物理理论和唯象方面，特别是非微扰量子色动力学、强子结构和计算物理。可以翻阅我的论著和开发，以及我最近的报告。

1973年建立的量子色动力学(quantum chromodynamics, QCD)是强相互作用的基本理论，它描述了夸克与胶子之间的相互作用，

QCD在高能标具有渐近自由，即耦合常数随着能标的增加而降低，这一特性使得微扰计算称为可能。但在低能标QCD是强耦合的，这带来了色禁闭和手征对称性自发破缺等非同寻常的非微扰物理，但也使得在低能标求解QCD无比困难。QCD的非微扰计算是物理中最艰巨的挑战之一，当今物理学中一些最重要难题与此有关，这些问题包括：

• 为什么实验上观测不到自由的夸克和胶子？

• 质子和中子的质量为什么远大于夸克的质量以及π介子的质量？

  束缚质子与中子的核力是如何形成的？

• 夸克和胶子在质子中是如何分布的？

• 所谓奇异夸克态的结构是怎样的？

• 核物质的相结构即其在有限温度有限密度下的形态是怎样的？

这些强子的非微扰性质是当代高能物理实验的焦点之一。这些实验包括，美国杰斐逊实验室12 GeV/24 GeV升级以及布鲁克海文国家实验室的电子离子对撞机 (EIC)、欧洲核子中心的LHCb与ALICE实验、惠州HIAF设施上的中国极化电子离子对撞机(EicC)、北京正负电子对撞机的BSEIII实验和日本KEK的Belle II实验、合肥的超级陶粲工厂(STCF)等等。

基矢光前量子化

基矢光前量子化(basis light-front quantization, BLFQ)是一个基于光锥哈密顿量形式理论来求解非微扰量子色动力学的理论框架。哈密顿形式是量子理论的基础理论框架之一，在物理中应用非常广泛。它是非微扰的，并且能够提供体系的所有结构信息，包括实时演化信息，体系的演化由薛定谔方程给出：

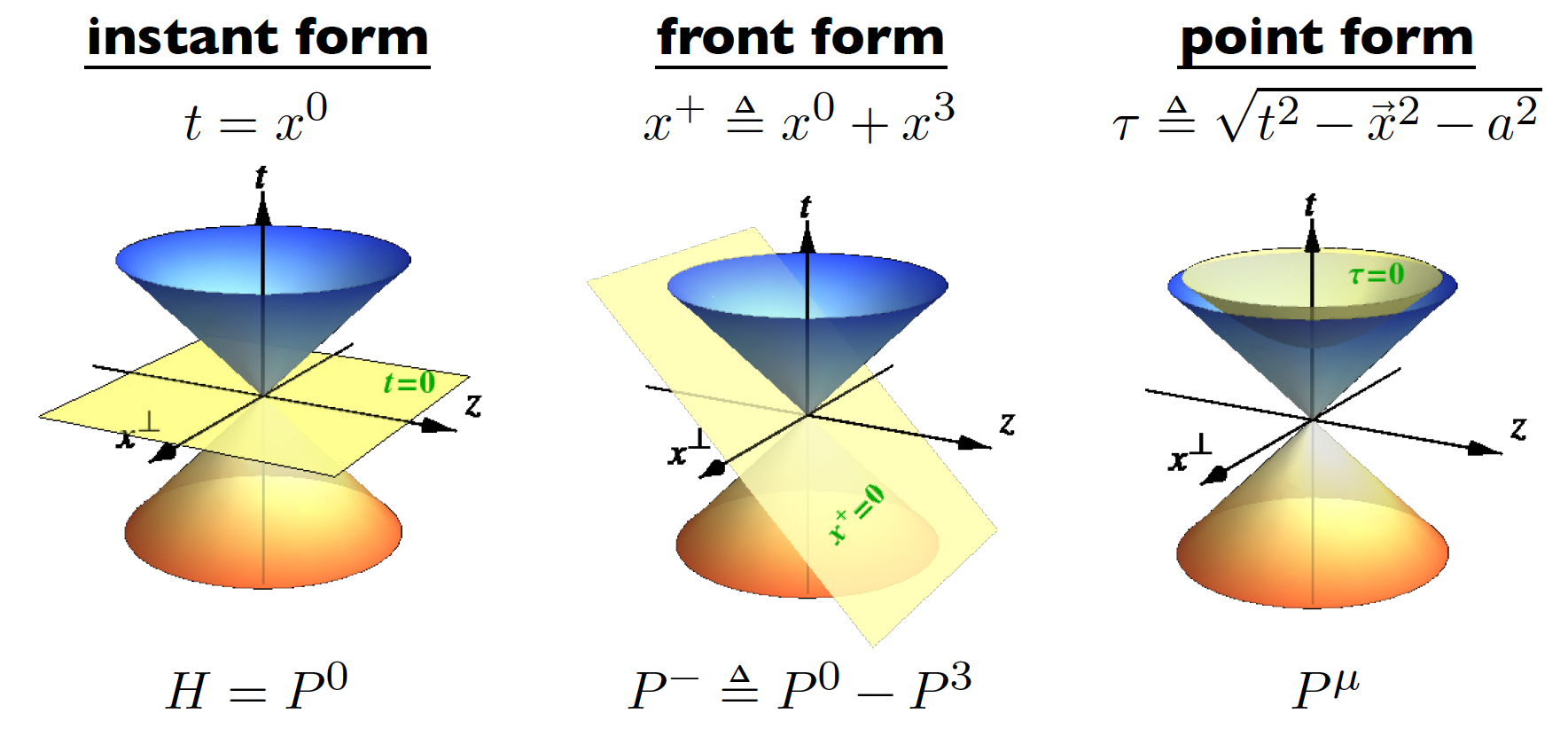
1949年，狄拉克提出的光锥动力学可以极大的化简相对论量子场论。所谓光锥动力学是指体系沿着光前时间x^+ = t + z/c进行演化，因此体系的波函数定义在与光锥相切的光前平面x^+=0上。光锥动力学是费曼部分子物理的基础与现代高能物理散射实验密切相关。

在光前哈密顿量形式理论中，强子的波函数由爱因斯坦方程给出：

其中，H = P_\mu P^\mu 又叫做光锥哈密顿量。 基矢光前量子化应用量子多体方法来求解光锥哈密顿量的本征值和本征向量。它选取一组基来保持光锥哈密顿量的对称性，并利用哈密顿量重整化方法和稀疏矩阵计算技术来加速量子多体计算。

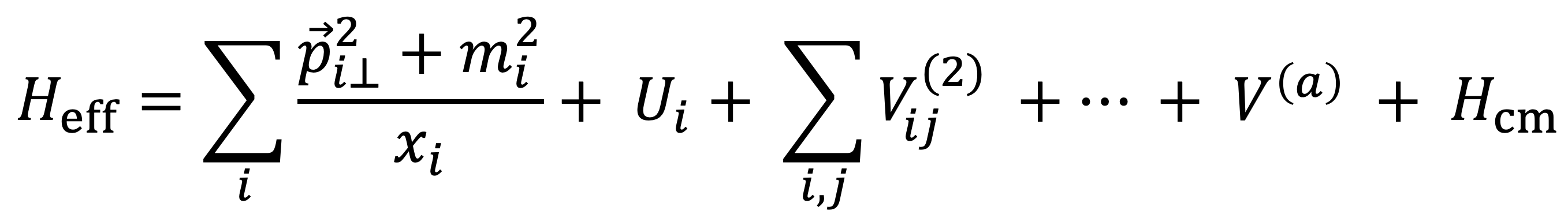
随着数值解析度的增加，希尔伯特空间的维度呈指数形式增长，这就是所谓的指数墙问题(exponential wall)。如何穿越指数墙得到有效的物理结果，是量子多体计算面临的最大挑战之一。 原子核物理中的无芯壳层模型(No-core shell model, NCSM)结合了体系的一级近似、稀疏矩阵严格对角化与哈密顿量重整化方法，提供了解决这一问题的一个可行的方案。基矢光前量子化将这一方法推广到强相互作用。 计算科学(包括量子计算)的发展提供了从第一性原理出发非微扰求解量子色动力学的良机。当然，QCD的独特复杂性意味着我们需要在计算和物理方面付诸努力，并将两者相结合，而这是我的研究的核心。

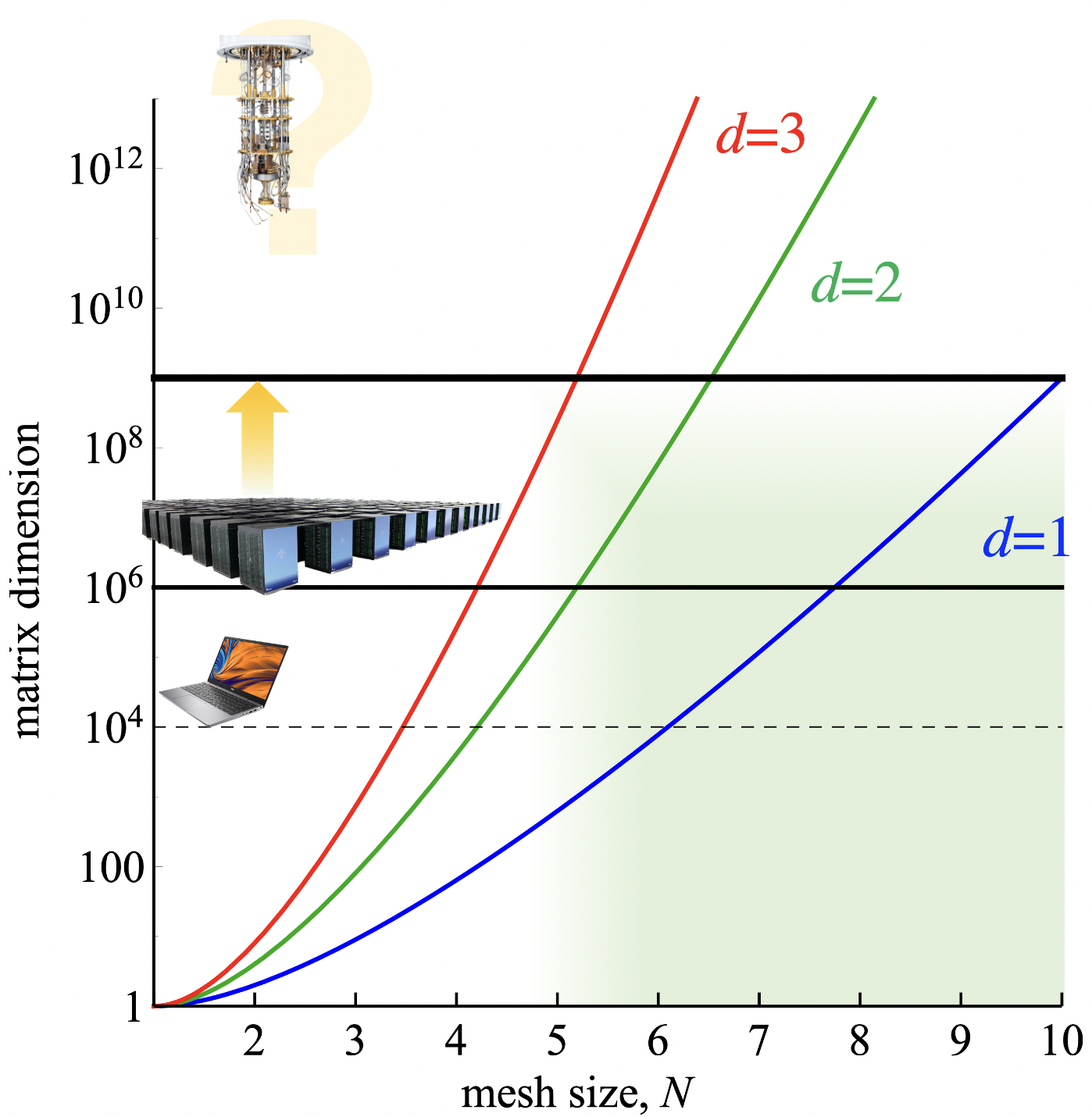
强子谱与强子波函数

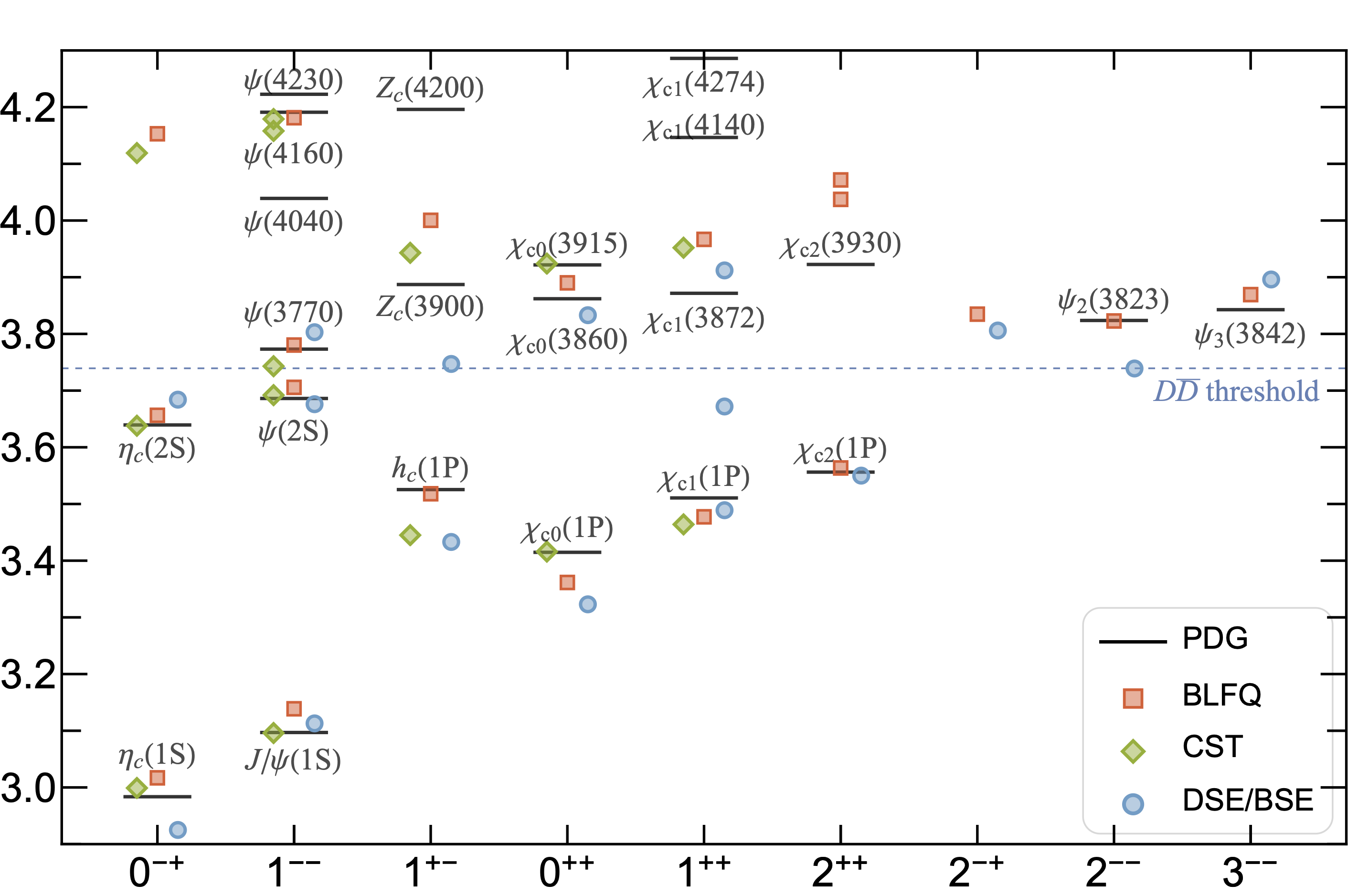
基于光锥全息量子色动力学和光锥量子色动力学，我们提出了一个相对论性的唯象强子模型，并采用基矢光前量子化方法研究强子谱。如图所示，在使用两个拟合参数的情况下，所获的的粲偶素质量谱与实验结果具有良好的符合。 对角化哈密顿量还可以同时获得高精度的光锥波函数，它们可以用来研究强子结构包括强子的部分子分布。一些介子(包括夸克偶素)的光锥波函数已经上传至Mendely Data。在此基础之上，我们还进一步增加动力学胶子和海夸克自由度，实现超越夸克模型的物理。

辐射跃迁与强子衰变

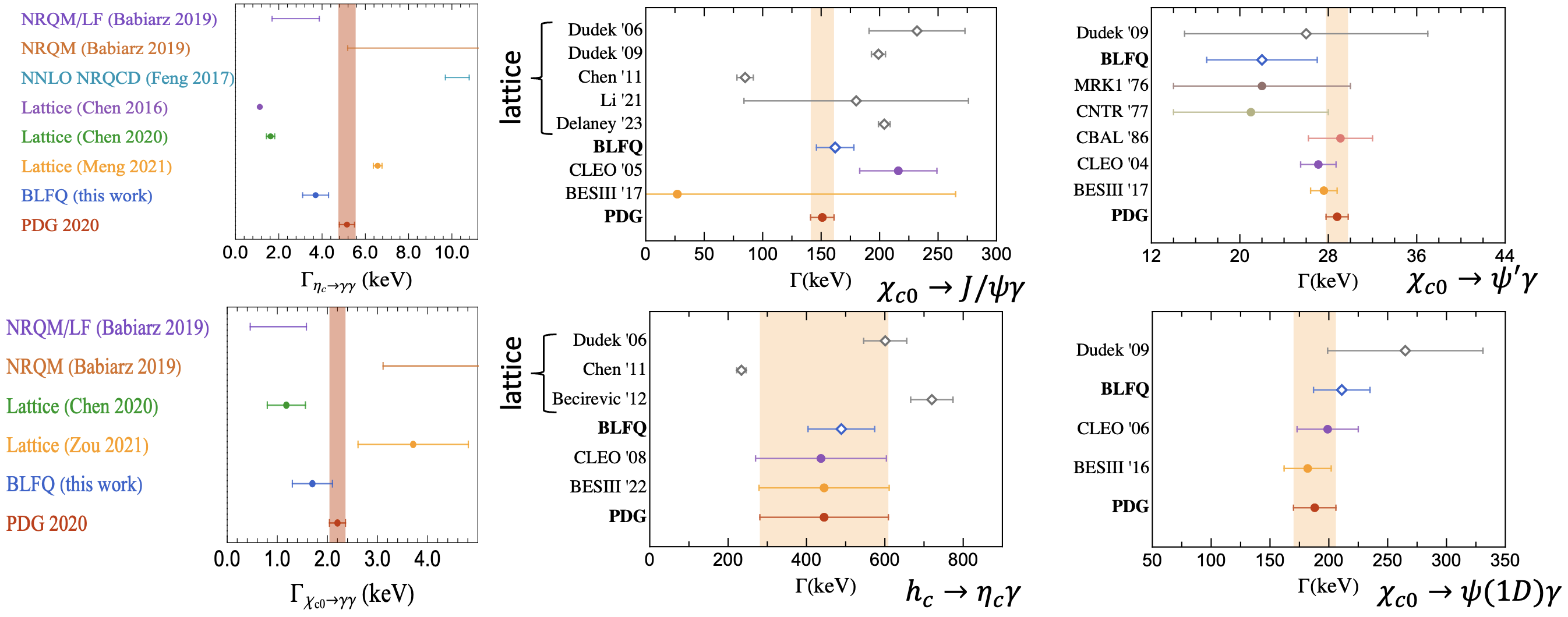
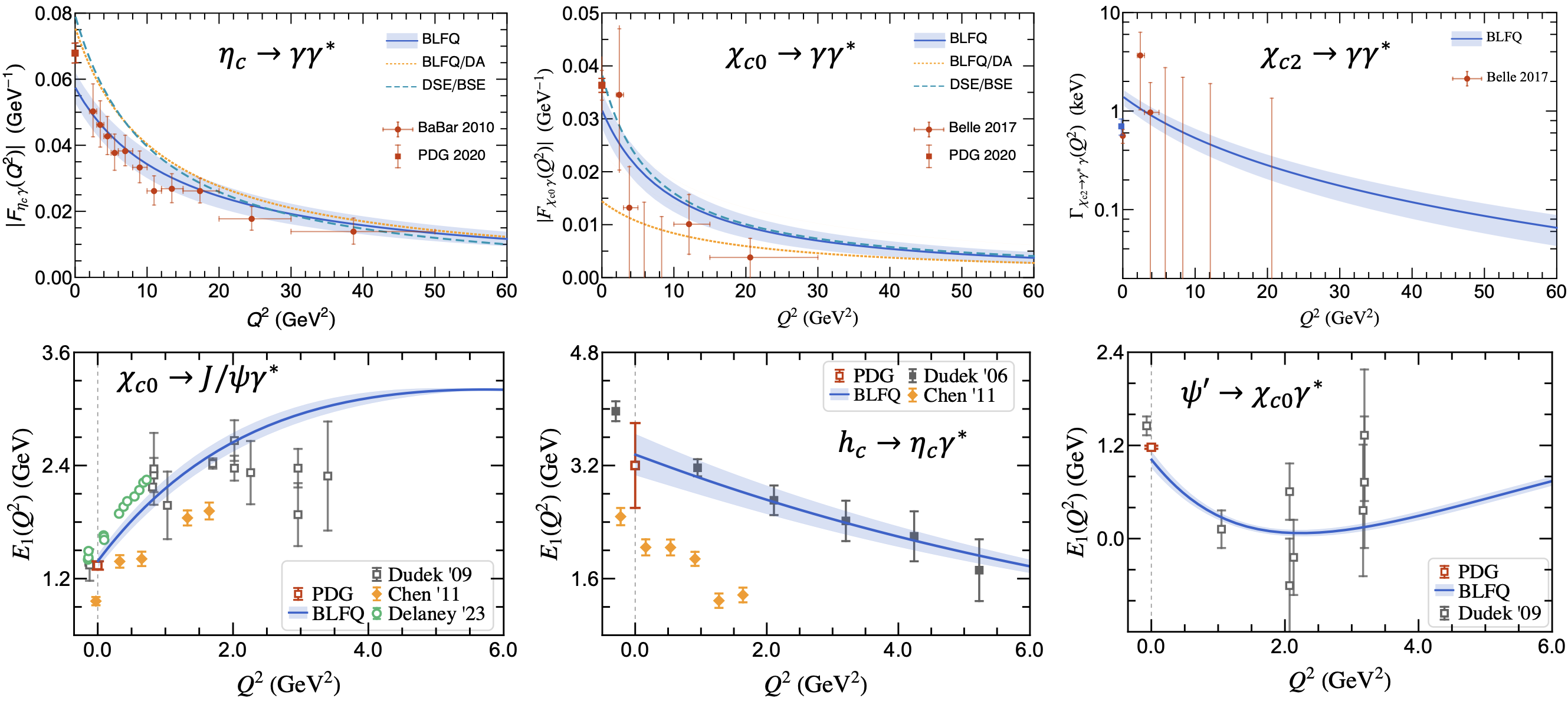
研究介子辐射跃迁可以揭示其内部夸克的运动和相互作用，从而加深对介子结构的理解。辐射跃迁与强子短距离的结构有关，因此可以检验强子波函数在短距离上的行为，而不同种类的辐射跃迁也可以探测不同角动量、宇称的介子。利用已经获得的光锥波函数，在不引入任何新的参数的情况下，我们计算了粲偶素的辐射跃迁振幅，并将结果与实验测量相比较。所得到的衰变宽度和跃迁形状因子都跟实验结果符合的非常好。这些结果展示了所得光锥波函数的准确性。

能动量张量与引力形状因子

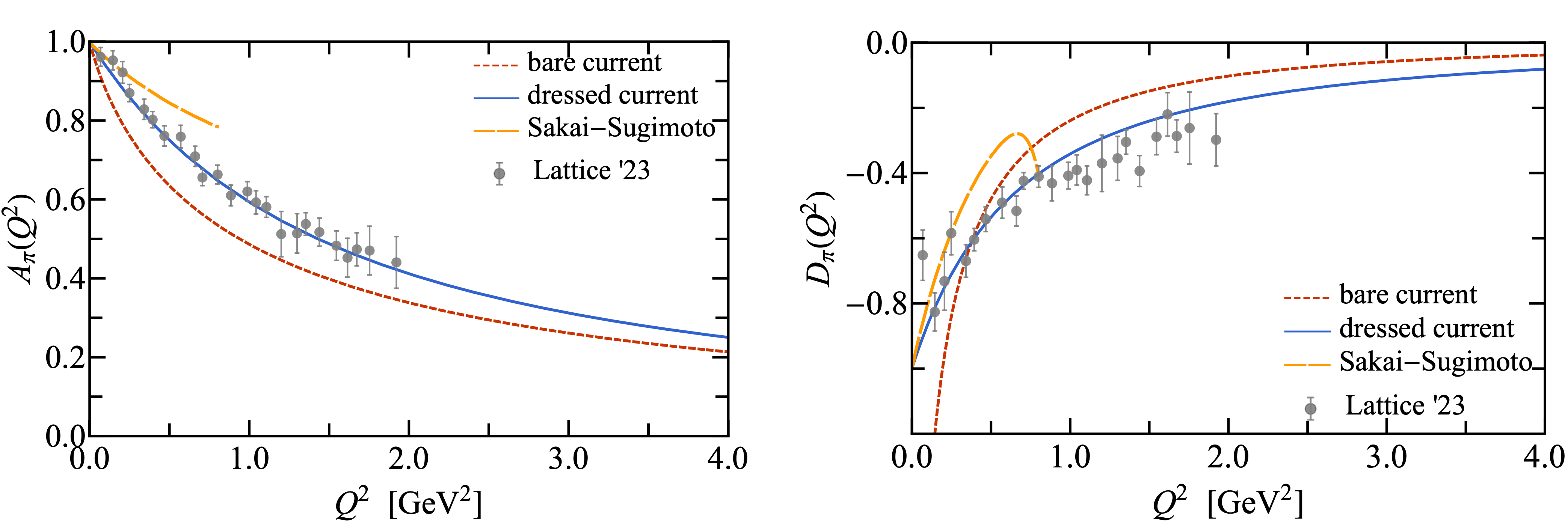
引力形状因子参数化了强子的能动量张量矩阵元，它们本身包含了强子内部能量、自旋和应力分布的信息，并且与强子的质量起源直接相关，还为了解色禁闭、强子的力学稳定性等问题提供重要洞见。但人们对于强子引力形状因子的了解还远远不足，尚有不少疑问和争议有待解决。 我们一方面提出了强子能动量张量的宏观解释，即将强子能动量张量与相对论性连续体能动量张量联系起来，给出每一个引力形状因子的物理解释。另一方面，我们还提出了能动量张量的微观波函数表示，从而解释了强子能量、自旋和应力的微观起源。利用这些波函数表示和全息量子色动力学，我们首次得到了π介子的引力形状因子。

非微扰重整化

非微扰重整化是求解强耦合量子场论问题的基本挑战之一。在哈密顿量形式理论中，由于显式协变性的缺失这种挑战变得更大。神奇的是光锥哈密顿量仍然能够保持簇分离原理，尽管所有的光锥费曼图具有严格的光锥时序。福克依赖重整化(FSDR)方法充分利用了这一点来发展一套针对福克空间截断的系统的非微扰重整化方案。FSDR已经被成功应用于一些(3+1)维的量子场论，包括汤川理论、标量场理论和量子电动力学。在这些计算中，自外发散被严格地消掉了。特别是在标量场理论中，最大福克空间可达3个修饰粒子，福克空间展开的收敛性得到了验证。