What we are working on: We are working on the theoretical studies of relativistic heavy ion collisions.

In order to understand the asymptotic freedom in strong interactions (also see 2004 Nobel Prize in Physics), T.D Lee (李政道, 1974) and Collins (1975) proposed to use the relativistic heavy ion collisions to creat a new form of matter, Quark-Gluon Plasma (QGP).

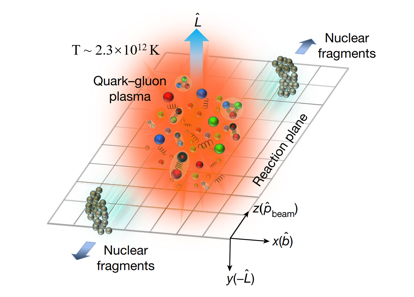
Very high magnetic fields and orbital angular momenta (OAMs) are generated in these collisions. The magnetic fields are on the order of 10^(17−18) Gauss and are the strongest magnetic fields observed in nature. The QGP is also found to be the most vortical fluid, where a huge OAM is transferred to the fluid in the form of vorticity fields. These novel phenomena open a new window for the study of the QGP in heavy-ion collisions. These novel phenomena are quantum in nature and are usually negligible in classical fluids.

(1) Quantum kinetic theory for massless and massive fermions

Kinetic theory can describe the phenomenon far away the equilibrium. The most well-known theory is the Boltzmann equations. In order to understand the quantum transport phenomenon for massless fermions, we have derived the chiral kinetic theory from the first principle calculations ( from quantum electrodynamics). We have implemented the Wigner function W(x,p), which the the two point Green functions under the Wigner transformation.The chiral kinetic theory is the kinetic theory for the massless fermions with quantum corrections. One of the most imporatant correction is related to the famous chiral anomaly. The Omega in the above equations is also found in the condensed matter physics, named the Berry curvature.

Applying the chiral kinetic theory, one can derive the macroscopic quantum transport phenomenon order by order, e.g. the chiral magnetic effect (disscussed in the topic "Matter under strong electromagnetic fields"), chiral vortical effect, chiral anomaly and other higher order electromagnetic responses.

(2)Quark matter under strong electromagentic and vortical fields

Very high magnetic fields and orbital angular momenta (OAMs) are generated in these collisions. The magnetic fields are on the order of 10^(17−18) Gauss and are the strongest magnetic fields observed in nature. 

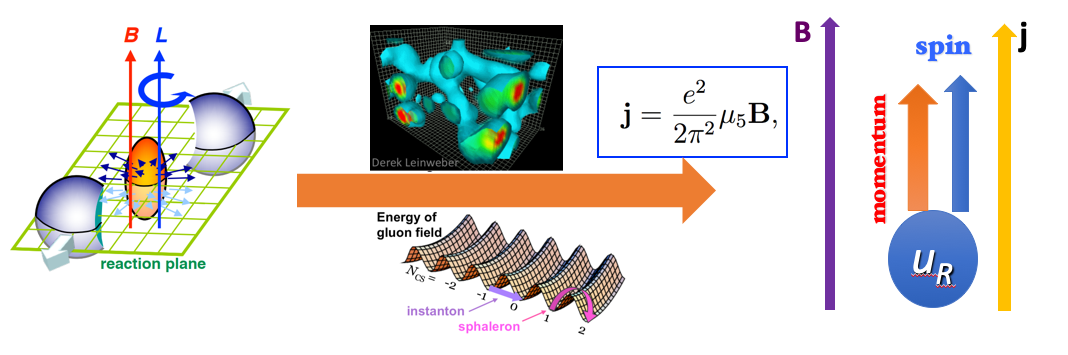
One of the most important quantum transport phenomenon is the Chiral Magentic Effect. The chiral magnetic effect (CME) and chiral separation effect (CSE) are two quantum effects on the magnetic field in a chiral fermion system. In the CME, a charge current is induced along the magnetic field, where μ5 is the chiral chemical potential. The magnetic field can also generate a chiral current, where μ is the charge chemical potential. These two quantum effects are related to the chiral anomaly, which is absent from classical theories. The chiral chemical potential represents a chirality imbalance. The nonzero μ5 arises from topological fluctuations in quantum chromodynamics (QCD), which are related to the local violation of parity and charge parity. Therefore, the observation of the CME in heavy-ion collisions implies local parity and charge parity violation. In addition, the CME has been observed in condensed matter and can be applied in quantum computing.

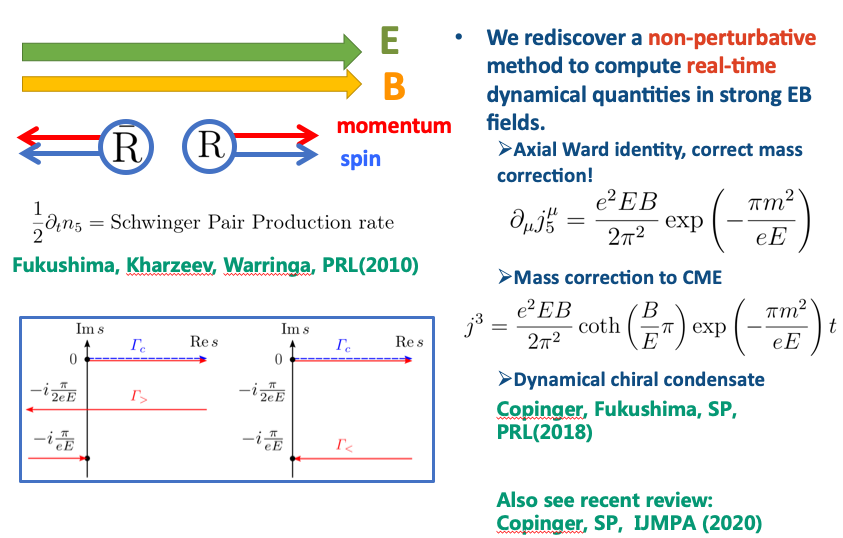
The mass correction to the CME is related to another well-known phenomenon, Schwinger pair production. The operator equation for the CME with finite mass corrections is the axial Ward identity. We have computed by the famous non-perturbative method, named world-line formalism, to compute these operators in the In-In states.

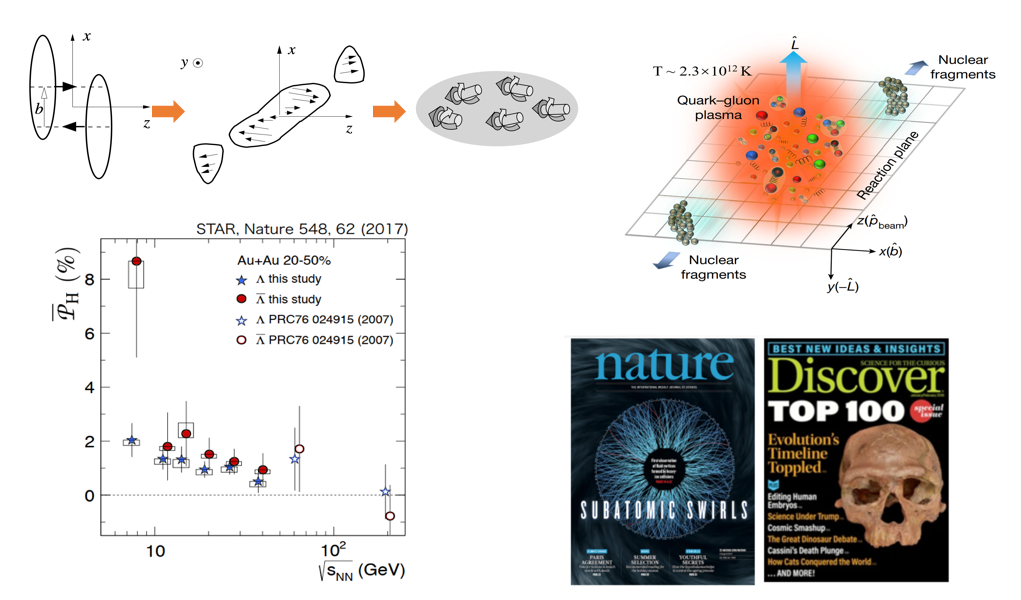
Another important topic is the spin polarization in the relativistic heavy ion collisions.