本学期教学
关于考试总评分数
大学生研究计划和本科毕业设计
那些让人眼前一亮的数学
如何了解现代的数学
如何选择研究方向和导师
数学是什么
关于教学的一些观点
研究生指导
关于读研究生的一般性建议
关于如何学习数论和算术几何
几篇旧文
关于代数几何的有趣讨论
关于 我具体研究的方向
关于跟我读研究生
关于如何写好基础数学的学术论文
关于写推荐信
做这个网页不是 为了让你们都来找我当导师，而是为了你不要来找我当导师：我一个人带不了那么多学生，水平也很一般，而且时间、精力都花在写这些东西上了没花到做学问中去。我本意是希望无论你是不是我的学生又或许我哪天不再当老师了，你都依然能从中受益一小点，并觉得数学很漂亮精彩迷人。只是这种工作在我花时间做这个网页时国内还少有人做，我暂时填补一下国内空白。
代数I（中法班大一）
这是一门为中法数学英才班设置的课程。是一年级的代数课程。使用法国原版预科教材。本课程配有每周4学时的习题课（Travaux Dirigés简称TD）以及一学期至少一次的口试训练（Colles）。
除教材外，参考书：
《线性空间引论》陈恭亮、叶明训、郑延履
《Cours De Mathématiques Du Premier Cycle》 Jacques Dixmier
GTM73、GTM211
参考法国预科一年级的2013版标准教纲，结合国内的教学情况，中法班委员会拟定了一份中法试验班的教纲。中法班的教学将保证至少覆盖标准教纲并尽量完成中法班教纲。具体教学内容和教学进度会根据学生学习状况反馈及时调整，而并不是盲目遵循预设的教纲，随后的教纲 根据教学经验结合实际调整。所以请同学们积极反馈，我们希望收集各类意见让中法班变得更好，可以以书面形式，发邮件，发微信或者写纸条给任何一位任课老师。
上课地点：5506
上课时间：2-18周，周一34节、周三34节
习题课时间：周一89节、周三67节（曹培根5506）
习题：求证存在一个多项式函数P(X,Y)，使得对于任何一个学生，X与Y分别代入期末卷面分和助教平时分后正好得出教务处存底的总评成绩。
注意：我从不给某一位同学单独调分，这对其他同学不公平。
如果想在课外了解一些与数论或者代数几何相关的知识，本科生可以申报学校的大学生研究计划（管理办法，流程），我可以指导（商定学习内容、提供参考材料、讨论数学、组织讨论班交流和汇报阶段学习情况）若干个学生（一般每年不超过四个）。一般而言，学习基础数学的本科生的科研活动经常是增进对一个领域/研究主题/前沿研究方向/经典理论/经典定理的了解，最终总结报告常常为读书报告，我会根据每个学生现有不同的知识结构建议合适的主题。 不过，在学术指导之外，我往往会不了解/记不住学校关于大研的各种deadline，教务处也不会定期提醒我，所以我需要你们提醒我各种时间节点，否则无法按照学校的要求按时结题。不过，如果你并不在乎这个，只是希望我指导你学习一点数论的知识，那我是乐意的。
2022-2023年指导的大学生研究计划：包文昊、谭午烜、芦嘉璇
2021-2022年指导的大学生研究计划：覃俊卓
2021-2022年指导的大学生创新计划项目：李子骏-周圣博-叶德意（校外合作导师：B. Keller）
2019-2020年指导的大学生研究计划：张寂之、何志强、朱子璇、肖宇
其实跟大学生研究计划差不多，最终形成的毕业论文很可能是一个读书报告。我可以自己带本校的学生，也可以在外校找好指导老师而我当校内的导师（前提条件是：论文的内容至少要跟我的方向相近，至少是偏代数的），还可以带校外的本科毕业生（前提条件是：确定了将来在科大读研究生且感兴趣的方向与我相近：数论与算术几何） 。希望由我指导毕业设计的同学请到我办公室面谈，并在开始前必须阅读本网页下方关于论文写作规范的指引。
2025年：杨文东
2024年：王一多、黄梓屹、王原；作为校内导师：谭午烜（胡永泉）
2023年：刘星宇；作为校内导师：赵伟龙（B. Keller）、周圣博（胡永泉）、覃俊卓（申旭）、范城玮（秦厚荣）
2022年：王应济、邬雄宇；作为校内导师：叶子逍（莫仲鹏）
2021年：刘煜凡、朱子璇、赵天鸿；作为校内导师：肖宇（肖梁）、肖子达（陈宗彬）
2020年：韩旭然；作为校内导师：单逸（Illusie）、胡益榕（田野）、孙梦舟（吴刘臻）；外校学生：黄凯（四川大学）、王胜（武汉理工大学）
2019年：尹宏旻、禹蒲阳
- 在北京把北京地图随便往地上一摊，总存在地图上至少一点，它对应的位置正是它所处的位置。其实不需要摊开，捏成一团也行，只要不撕破地图。 （Banach不动点定理，分析）
- 地球上总是有一点没有风，或者说人的头发总会至少有一个漩涡。（hairy ball theorem，拓扑学）
- 赤道上总有一对对径点两地温度相同。地球上总有一对对径点，两地的温度和气压分别相等。（Borsuk-Ulam定理，拓扑学）
- 没有办法通过尺规作图做出一个正方形使得其面积和给定的圆一样。（Galois理论，代数学）
- 不存在一套程序性的办法用尺规作图三等分任意给定的角。（Galois理论，代数学）
- 五次以上的一元多项式方程不存在通用求根公式。（Galois理论，代数学）
- 在绳子上的蚂蚁喝醉了酒左右乱走它有100%的机率回到出发点；在地面上的醉汉随便走也有100%的机率回到原点；不幸的是在天空中喝醉了酒的鸟乱飞回到原点的机会大概只有34%。 （Polya随机游走常数，概率论）
- 2的n次幂的十进制表达的首位是数字k的概率是lg(k+1)-lg(k)。（遍历理论）
- 无论假定了什么条件，总存在一个命题，没办法证明它是对的也没办法证明它是错的。然而，前面这句话不是瞎说，已经被严格证明了。 （Godel不完备定理，数理逻辑）
- 周期三意味着混沌：闭区间上到自身的一个连续映射如果存在一个周期为3的点，那么对于不可数无穷个初始点在此函数迭代下的序列是杂乱无章的。（李天岩-Yorke定理，动力系统）
- 地球上任何一张简单地图只需要四种颜色就能够把两两相邻的地区区分开。而在环面上则需要七种颜色。（四色定理，图论）
- 这世界上的正多面体仅仅有五种。（拓扑学）
- 光滑射影三次曲面上正好有27条直线。（代数几何）
- 每个正整数都是四个整数的平方和，每个有理数都是三个有理数的立方和。（数论）
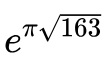=262537412640768743.999999999999...（数论）
如果想了解现代的数学有哪些领域，是如何分类的，可以看看这里Mathematics Subject Classification。虽然其中并没有什么实际的数学内容，但是可以让你瞟一眼整个数学大概有哪些方向和专业。如果你不理解其中的名词，可以考虑查一下百科全书（例如维基百科），了解更多的信息。如果想了解得更多，可以看一看各届国际数学家大会里头有哪些分组，里头人们关心什么问题。例如2018年巴西里约热内卢的ICM。
二十世纪初David Hilbert在国际数学家大会上提出了23个问题，引领了数学发展一个世纪，二十一世纪初克雷数学所也提出了千禧年七个数学问题。学好了本科的数学课程之余，开阔自己的眼界也是十分重要的，这七个问题的陈述并不是太高深，在本科课程的基础上想要了解相关的内容并不算十分困难。
选择研究方向首先是要了解一点点这个方向，那就回到上面一个标题“如何了解现代数学”。上面给的建议基本上是站在一个本科生的角度也许可行的方案。但是其实我对数学的了解，往往是我读书的过程中（包括本科、硕士、博士）和一些跟我方向相距甚远的人闲聊数学中听回来的，听着同事或者朋友给我科普一些方向。也有些是偶尔参加一些简介性的讲座学来的，就像我在科大也会偶尔去听一听给华班学生开的华罗庚讨论班的课程，这些科普的报告对我也是有益处的。所以往往在需要选定一个方向的时候其实对数学的了解甚少，只能凭感觉，同时带上一点运气来选。
选热门方向还是冷门方向？首先如何区分热冷门，大概可以看今年ICM的获奖人是什么方向的，看看一小时大会报告是哪些方向，这些都意味着这是近期取得相对比较大的突破、涌现出新方法的方向，会是近期（也许是近十年）比较热门的方向。热门一定比冷门好吗？似乎也说不准，很多人加进去做当然意味着会有更多新的思想，是新学问的增长点。但做的人多了同时也将会是竞争比较激烈的方向，是否更容易取得成功，是否毕业后更容易找到工作，这些都不得而知：冷门的方向全世界做得人不多，找工作时相近方向的职位就会少；热门的方向又有可能同一个吸引力大的位置有十几二十个方向相近的同行竞争。
再进一步的了解一个方向的办法就是去翻一翻这个方向的著名论文（例如在“四大”数学杂志按章MSC分类来找找相关的方向近期的文章），当然读懂摘要和引言的机会很少。但是可以看看整篇文章大概是什么样的风格的，全是不等式还是都是抽象符号，是式子、符号长的你顶不住了还是有几个漂亮的图片。看这些基本读不懂的东西其实只是看看自己能否接受和这样风格的数学相处。
多征求身边各种老师的意见，即使他们不见得懂你想学的方向，但他的经验至少比你丰富，见识比你广，他一定见过身边的无数成功与失败的案例。
选导师（指博士导师）和选方向往往是同时的，或者选导师比选方向稍微晚一点。选有名望的老教授还是选年轻人？这也是个玄学：年轻人相对精力充沛、活跃、问题多、往往更接近前沿，有名望的老教授也许在你毕业时能够利用他的影响力帮你找到一份好的工作。其实如果你并不是很出众的学生，选择不是特别多的话，谁愿意要你你就跟谁吧，这也是看缘分的。当然选定一个导师之前可以做以下几件事情：到数学家谱上查一查这个门派里有哪些人，或许有你认识的。问一问周边的人这位导师的口碑如何？是不是曾经有很多人没能在他那里毕业？（不过这也不能完全怪老师，跟学生的表现也有关系。）咨询一下这位导师曾经的学生，他是如何带学生的，是不是能够有足够的时间投入给学生。上网搜一搜这位导师的学生毕业后都去什么地方工作了，是不是还都留在学术圈。
-
傅里叶先生认为，数学的主要目的是服务人类，解释自然现象；但像他这样的哲学家应当知道，科学的唯一目的是为了人类心智的荣耀，因此，一个关于数的问题与一个关于宇宙体系的问题具有同样的意义。——C.G.J.雅可比
- 这些天拓扑天使和代数恶魔为了每个数学领域的灵魂而战。——赫曼.外尔
- 是否有想过谁是你心目中的英雄？我读本科的时候流行上bbs，看到了这些文字：Heros
in my heart 作者后来去了巴黎和普林斯顿念书，现在回国当教授了，猜猜他是谁？
- 数学情歌？由The Klein Four组合演唱的
Finite simple group of order 2.（歌词）读完本科的同学应该能理解歌词里头大部分的一语双关。
-
仿佛来自虚空——亚历山大.格罗腾迪克的一生 感谢我们学院的欧阳毅老师把这篇好文介绍给了国内读者。菲尔茨奖得主Laurent
Lafforgue于2019年的一个采访：
Génération
Grothendieck（格罗腾迪克一辈）（法语）。
- 美丽心灵 A
Beautiful Mind 电影改编自真实故事，主人公：约翰.纳什（诺贝尔经济学奖得主，领完Abel数学奖之后回家的路上车祸去世，唉！除了博弈论，他在数学上有名的贡献是纳什嵌入定理：任何一个黎曼流形可以等距的嵌入到欧式空间）
- 人类花了350多年去证明了一个方程没有非零解——Fermat的最后定理。纪录片
- 中国剩余定理
三人同行七十稀，
五树梅花廿一枝，
七子团圆正半月，
除百零五便得知。
- 如果要问一个数学家什么最重要，回答可能不是别的，而是粉笔。
- 尼古拉.布尔巴基的讣告（出自作家Jacques
Roubaud）想要发现里头的双关语，需要多学一点数学，和法语。这儿有关于他生前的更多故事。
Faire-part de décès
- Les familles
- Cantor, Hilbert, Noether,
- Les familles
- Cartan, Chevalley, Dieudonné, Weil,
- Les familles
- Bruhat, Dixmier, Godement, Samuel, Schwartz,
- Les familles
- Cartier, Grothendieck, Malgrange, Serre,
- Les familles
- Demazure, Douady, Giraud, Verdier,
- Les familles
- Filtrantes à droite et les épimorphismes stricts,
Mesdemoiselles Adèle et Idèle,
ont la douleur de vous faire part du décès de M. Nicolas Bourbaki, leur père, frère, fils, petit-fils, arrière petit-fils et petit-cousin respectivement, pieusement décédé le 11 novembre 1968 (jour anniversaire de la victoire) en son domicile de Nancago.
L'inhumation aura lieu le samedi 23 novembre 1968 à 15h au cimetière de fonctions aléatoires, métros Markov et Gödel. On se réunira devant le bar « aux produits directs » carrefour des résolutions projectives, anciennement place Koszul. Selon le voeu du défunt une messe sera célébrée en l'église Notre-Dame-des-problèmes-universels par son éminence le cardinal Alephun, en présence de toutes les classes d'équivalences et des corps (algébriquement clos) constitués. Une minute de silence sera observée par les élèves des écoles normales supérieures et des classes de Chern, car « Dieu est le compactifié d'Alexandrov de l'univers » (Groth.IV.22).
大学的学习和中学是很不一样的，更多需要的是自觉和自我督促。我不会监督你学习，我上课从不点名，只要来上课的剩下一名学生我的课程都会继续。我并不认为上课听课并跟随老师的思路适用于所有学生，但是这确实适合绝大部分学生。你可以觉得你就是那个例外，自己做出的决定自己承担后果/享受成果。我的一般建议是去听课，听不同老师的课，了解不同的切入点；去看书，看各种相关的书，了解不同的处理方式。我的考试难度已经非常低，只要花心思学了课的同学（努力完成每一道习题，和同学与助教讨论习题），通过考试是不成问题的。对于某些“基础课程”，就是说内容设置是你这个层次的学生应该掌握的，我会偏向于以很快的速度“灌”给你们，从而避免到最后由于课时不足被迫放弃掉一些基本内容。这种时候我必定不可能照顾到所有人。如果你听不懂了，要打断老师的讲课问问题，尽全力拖慢老师上课的速度，而不是简单的逃课，当然逃避是“解决”问题的最简单办法。我从不假设考进了大学（或研究生院）就能毕业，本来就有一定的淘汰率，只是现在的学校或者是社会风气并不像过去那么严格要求大学生（所以“大学生”这个头衔就烂大街啦，博士毕业也找不到满意的工作啦）。往往看到不及格率太高还要从各个方面给任课老师压力，要求放水。如果老师作为最后把关的人而不严格要求，那更难以培养出真正合格的学生。在我的考试中如果你总评分数是60的，意思是你这门课并没有及格，说句实话我更愿意把考试原始分数直接上交。
如果你讨厌一门课，那你可以不修。如果它又是必修而你又觉得课程设置不合理，你可以提出你的建设性的建议。但是，请你先考一个像样的分数，至少得及格，否则你的意见不会有人重视的。我记得我出国第一年参加的一个代数和数论的项目，但是必修一门辛几何的课程，我很不喜欢很不乐意且意见很大。但我最后考试拿了满分，而我也不知道最后我的意见有否被采纳。你要想提出能得到重视的建议首先要排除掉“你太弱了不想修那门课才提意见来避免修课”的因素，因为或许这门课程的设置就是为了锻炼你数学的某方面的能力而这方面正是你所欠缺的而又是必须的。
我教的课基本是跟代数相关的。国内目前大部分高校代数学相关的课程要比分析学相关的课程少，你只要数一数你本科修过的课程和将要修的课程就会同意我的判断。也许，某些时候你会觉得我的课程偏难了，那可能是因为你的代数知识太缺乏。代数和分析是数学里两个方面，风格截然不同，分析具体但繁琐而代数简洁但抽象。处理这两种对立的风格的能力都是数学能力的重要组成部分，缺了哪个都是数学没学好，也因此可能毕不了业。我认为，本科毕业以前分析和代数应该是要均衡的发展的，这是本科数学相关专业应该培养的基础素养，也都是以后研究生学习的基础。类比的说，你可以是一个右撇子，但你的左手也得是能干活的，当然我不排除杨过的存在，如果你真是杨过的话我会给你点赞。由于代数天生抽象，一上来总是一大堆新的概念，一开始总是十分枯燥难懂。但这是学习必经的阶段，等你学懂了Galois理论，会发现代数能够解决尺规作图“化圆为方”、五次以上代数方程没有通用的求根公式这些听起来简单有趣但又十分深刻的古典问题。这样的结果可能是本科阶段能见到的最漂亮的结果之一。 尽管有如此精彩的理论，依然有人会觉得抽象代数/近世代数这门课并不是对所有数学相关专业都“有用”。我的观点是：学习代数课程最终目标并不是让你对群、环、域的结构有多么深刻的理解，而应该是让你体会如何用抽象的力量去解决刚刚提到的那么具体的问题的独特办法。从小到大的教育之中对抽象能力的训练实在是太薄弱了。等你读懂了Galois理论、了解了拓扑的基本群、学明白了黎曼面和覆盖空间，Grothendieck的SGA1（Séminaire de Géométrie Algébrique）告诉你其实Galois群和基本群是同一个事物的两个极端侧面，我觉得这是数学史上最为精华的部分之一。想了解这些人类心智的荣耀，代数 （抽象）、分析（具体）、几何（形象），缺了哪一方面的基础知识和基本能力就无法做到。总结：不要抱怨代数太难了，事实上是你太缺乏代数知识和代数思维的训练。
其中曹阳老师（个人 主页一、二）2020年也到科大工作了，在科研和指导研究生上我们会有很多合作，例如一起组织讨论班、会议、共享各种信息和资源、谈论学生八卦等。想读我们方向的研究生可以同时多和他交流或者成为他的学生 ，他数学比我厉害而且暂时他的时间更充裕。如果你已经来到中国科学技术大学读研，数论、代数几何等相关方向我们学校的导师还有：欧阳毅、盛茂、张磊、刘永强等等。
博士生
08-刘星宇（2023/硕，2024转博/未知）
07-汪立言（2022/直博生，与山东大学曹阳、首都师范大学赵斌共同指导<因曹阳离职2024转至我名下>/未知）
06-胡旭彬（2020/硕，2022转博<与马立明共同指导>/未知）
05-刘煜凡（2021/硕，2022转博/未知）
04-黄凯（2020/直博生，2020硕，2021转博/未知）
03-章辉（2019/硕，2020转博/未知）
02-胡广（2018/硕，2019转博/2023年末毕业2024到山东大学博士后）
01-吴晗（2018/博，2019起和徐飞共同指导/2022毕业到湖北大学工作）
硕士生
13-李嘉良 （2023/硕/未知）
12-张子扬 （2022/硕，与山东大学曹阳共同指导<因曹阳离职转至我名下>/2024毕业）
11-王应济 （2022/硕/2024毕业）
10-刘镇谋 （2022/硕/2023转博：导师杨金榜）
09-乔洪涛 （2021/硕/2024结业）
08-季善为 （2021/硕/2023毕业）
07-王胜（2020/硕/2022毕业）
06-韩旭然（2020/硕/2022毕业）
05-王崇宁（2019/硕/2020转博：导师张磊）
04-陈林（2019/硕/2021毕业）
03-禹浦阳（2019/硕/2021毕业到复旦读博士，导师：江辰）
02-方日鑫（2019/硕/2021毕业到复旦读博士，导师：王国祯）
01-陈志春（2017/硕，2018年转到我名下/2020毕业）
Université Paris 13 et
ENS Cachan
Andjor Mohamed(2016/Master
2/未反馈)
菩提老祖对孙悟空说：“日后惹出祸来，可别说我是你的师父。”我深以为然！
主要报告人是我们的硕士研究生、博士研究生、博士后，主要面向对象是研究生，同时欢迎感兴趣的高年级本科生参加。讨论的主要内容：我们方向的具体的科研文章、我们方向的入门内容、以及一些不出现在研究生教学中的又与我们方向相关的内容。每一次报告的内容不一定连贯，内容的难度差异也可能比较大。一般在学期中每周周期性的进行，具体时间地点会根据我们出差实时调整灵活安排，由于信息更新比较频繁，采用微信群通知。感兴趣参加的可以私下加微信入群。
Bjorn Poonen教授的一些建议。我觉得写得挺好的，关于选择导师、写推荐信、发文章、找工作等方方面面，开始读研究生之前应该先来了解一下。
Ravi Vakil教授招收博士生之前需要了解的在这儿。这个链接一开始介绍了他招博士的基本要求，我招学生的要求明显没有那么高，很多我自己都做不到，但我相信我的学生一辈会比我更出色。后半部分谈到很多关于讨论班、作报告、写文章等等的建议都很有价值。
Terence Tao作为一个数学家关于职业生涯的各种建议。我都没看完，但有空的时候读一读，会有很多收获的。
Gian-Carlo Rota : Ten lessons I wish I
had been taught.
John Baez : Advice
for the young scientist
Peter J. Feibelman 出版了一本书：A PhD is not enough!
介绍了不少关于如何在科学界生存的建议，其中有很多适用于数学界。
上述这些能看到的基本都是一般性适用于数学学术圈的建议，无论是在国外或者国内，这些道理是普适的。关于国内，我小小补充一点个人体会，各位同行看到了如有不认同的欢迎私聊。关于未来的职业规划，作为学生需要事先有一点点了解以至于不盲目。目前（指2019年初）国内的数学水平还和国际先进的水平有明显差距，所以评判一个应聘者（应聘博后或者高校教职）水平的时候作出独立判断仍相对比较困难，换言之是难以找到真正十分懂行的专家来评判好与坏。退而求其次，数数文章数、看看文章发表的杂志的档次、看看独立科研工作有多少、看看求学经历一直到博士后是不是一路名校，不是特别公平但似乎也一下子找不到更合理而且高效的办法。不公平全世界都存在的，想要在学术圈找到自己满意的工作最重要的还是能有一些拿得出手的科研成果。其次，对自己的水平有客观的认识也很重要。在我读本科的那个年代，国外大学毕业不久的博士就能直接进985高校拿到副教授甚至教授，而到了现在，你得是从本科起到博士一路名校而且博士后做出不错的科研成果才可能评上国家的人才项目，即便如此不少985高校也不见得能提供一个固定的岗位了。一方面，留学国外的博士毕业生越来越多，愿意投身科研事业的年轻人逐渐增多，所以现在在有意回国服务的人之中能挑出很多名校毕业的优秀博士了，我们国家的科研水平一直在进步。另一方面国家经济发展了也愿意投入更多到科研和教育上，所以才有了大规模的海外留学归国潮流的出现。但是大学的规模不可能无限制扩大，国外相对成熟的教学和科研体制都实行了聘期终身制（tenure track），要有人退休/去世/升职/辞职才会有新的职位空出来。目前国内在很多高校逐步展开的聘期制也不是这个的完全照搬，一方面职位可以终身但待遇并不一定终身，另一方面又可以建设很多新的研究中心/研究所/实验室来“无限”增加职位的数目。所以正要开始读研究生的同学们，你们要预想毕业的时候学术圈的就业市场是怎样的，大概是现在欧美的聘期终身制和我国国情的某种“奇特的融合”。限制到基础数学，还有许多特殊的地方。不像很多需要做实验的科学，加大了财力的投入建设大型实验设备，科研水平就有显著的提升，数学特别是基础数学需要的是人类的智慧慢慢往前推进。研究水平上国内外的差距需要更长的时间需要好几辈人的努力才能慢慢缩小哪怕一点。这个年代也许无需再为中华之崛起而读书，但还需为中华之复兴而奋斗，如果你还年轻请怀揣一颗赤子之心埋头苦干。
学生们常有疑问：博士怎样才能毕业？按我的理解，在理想状态下，大致标准应该是学生在某一个地方超越导师一点、能够做出一点导师没能想到的东西（哪怕只有那么一点点新颖的地方是出乎导师意料之外）的时候。具体的规则每个学校不太一样，但我觉得套一套上面这个标准基本上是合适的。所以，在数学研究水平越高的大学/研究所博士毕业一般也就越困难，博士学位的含金量一般也越高。
我为什么选择了代数几何和数论（写于2012年12月16日 巴黎）
怎样熬夜做数学（2013年11月13日）
尾声（2011年7月11日）
关于ALGANT项目的体验（已经忘记是什么时候写的，作为ALGANT硕士项目的校友被邀请写下的）
芝加哥大学的Matthew Emerton教授收集了一些跟代数几何相关的有趣的讨论，挺有意思的。
也常常有同学希望学习某个专题让我推荐一本参考书，我确实可以推荐我自己喜欢的书。但是，我从根本上认为其实读哪本书并不是十分重要，重要的是那套理论所包含的基本内容。没有一本书会是完美的。不一样的书会从不同的角度去理解和讲述同一件事情，不同的书适合不一样的读者。所以往往我推荐完我自己喜欢的书之后，我的最终建议总是：你觉得哪一本书容易读懂，那就是对你胃口的，应该就是对你而言最好的书。
学校关于研究生毕业的基本要求和数学系的具体要求在这里和这里（可能文件的版本已过时，请自行搜索最新版）。跟我读研究生的毕业和获得学位的要求跟学校最低要求一致。
我指导学生的一些前提条件如下，请觉得自己满足要求（或者满足其中大部分、或者觉得自己很有可能在关键的时间点达到这些要求）才和我联系。
-1. 本科毕业应具有的数学知识结构：
我认为一个优秀的基础数学本科毕业生应该学过（包括自学）的课程/内容有：
a.分析方面：数学分析、实分析、复分析、泛函分析、微分方程
b.代数方面：线性代数、抽象/近世代数、同调代数、交换代数、群表示论
c.几何方面：经典微分几何、点集拓扑、代数拓扑、微分拓扑、微分流形
d.数学软件：LaTeX（包括制作ppt）、至少一门编程语言
e.外语：至少掌握一门外语，能看懂外语专业书籍、可以用外语书写数学，如果能用口语交流数学会更好。
简而言之：分析、代数、几何三方面的知识结构应该均衡，虽然不见得你以后的科研要用到所有这些内容，但这是你往后走的基础，站得高才可能看得远。
如果你已有的知识体系严重偏向于分析方向，我非常不建议你选择代数数论、代数几何这样偏代数的方向。并不是说完全不可能，只是说你需要补充的知识太多太多，等你补充完了之后其他同学又已经前进了一大步了。如果你想联系我读研究生，请你首先自己判断自己的知识体系偏向于哪个方面。由于近年来（2020年左右）每年都有很多同学向我咨询，如果你的代数方面学得少，那是不可能在我这里读研究生的，我会优先选择对代数了解更多的同学。
对代数感兴趣并不能成为你联系我当导师的一个有说服力的理由：如果你是真的对代数感兴趣，那你应当自学过很多（包括我没提到过的）代数的内容。你只需要介绍你自己学过的内容、看过的书，从你的知识结构我自然会知道你对代数、数论、代数几何有多感兴趣。
0. 总的要求：
我的研究方向是 代数数论 和
算术代数几何。分析和代数的风格很不一样，两者相比你要比较喜欢和习惯代数的思维和推理模式，而且你要比较擅长代数。
对于“擅长”每个人的理解不一样，我的意思大概如下。本科阶段应该了解的代数方面的知识大概包括：线性代数，群、环、域的基础知识和基本定理，Galois理论，代数拓扑（基本群和万有覆盖空间、同调群）。更进一步的我认为对学习这个方向有帮助的内容如下，这些内容大部分高校设置的本科课程和随后的研究生课程一般不会讲述，但对于掌握了基础的抽象代数和点集拓扑的本科生，以下内容是容易自学的：拓扑群的基本概念，域扩张的更进一步的知识（超越扩张、linear
disjointness等），无穷维的Galois理论。
还有一些与我的方向相关的，本科基础课程过后比较容易自学、往往会出现在低年级的研究生课程中的：初步的同调代数、初步的交换代数、初步的代数数论、初步椭圆曲线、初步的群表示理论、模形式，如果有时间也可以尽早了解。如果你还在读本科，打算以后学习我的方向，请抓紧时间了解以上内容
，反正这些内容基本不会有人教你而你迟早也躲不开。
说句实在的话：研究生的学习可能跟本科很不一样，对研究生而言自学能力是十分重要的（以后读科研文章就是一种更“高级”一点的自学），如果对上述提到的早已经成型并且已被改写得非常成熟的经典内容都不能自己学懂，那你应该质疑自己是不是有足够的能力日后读文章。如果你刚开始你的研究生第一年：(1)你想读两年制硕士，上述提到的内容（或者相似难度的内容）的读书报告可能成为你的硕士毕业论文
，也很有可能是某些近期的文章的综述报告。(2)如果打算跟我读博士，那你应该在转博之前至少了解这里提到的内容（这当然还远远不够，仅仅是“至少”）。
另外，关于几何方面的基础知识：了解微分流形的基本定义有助于日后帮助理解概型的定义。
1. 两年制硕士：
基本上科大基础数学只收这种硕士，我也收，而且没有名额限制，但要取决于我自己是否有足够的时间和精力。这同时意味着我不太可能花很多时间在你身上。一开始你需要告诉我你学过什么课程，我会告诉你哪些研究生课程适合你，一年之后根据你的课程成绩和各方面知识掌握的程度给你找一个难度相对适合的硕士题目。一般是看一本书或者一篇（几篇）论文，你的硕士论文就是一个读书报告，向同学们介绍整个故事情节，以及补充理解这个故事概要中出现的新概念所需要的预备知识的总结。我不可能具体和你讨论某个教材里某个具体的习题怎么做，这些应该和任课老师及助教
或者同学讨论。在硕士论文准备的过程中遇到的问题我会给你适当的书或文章作参考。过程中如果有问题请主动找我讨论，我不督促学生学习，但是如果你自己不积极主动，到了最后阶段才发现写不出论文或者把论文写得一塌糊涂那我就实在没法帮你了。获得学校的硕士学位的要求：无需发表学术论文，修满37学分（含学校公共必修
政治英语7学分和开题报告2学分），而且基础课（MATH5开头的课程）平均75分以上。若平均不足75，只能毕业，不能申请硕士学位。
（这些具体的规定学校不断在更新，请自己了解最新的要求。）
2. 三年制硕士：
科大基础数学大部分老师不收，可能有我不了解的例外。获得学校硕士学位的要求：需要已发表（或被接收）的学术论文，修满31学分（含学校公共必修7学分），而且基础课（MATH5开头的课程）平均75分以上。由于三年内要发表论文，我的方向几乎不可能，至少我自己读书时就没做到，所以我不敢收
三年学制的硕士生。
先提示一下获得博士学位学校官方的要求，修满45学分（含学校公共必修 11学分），而且基础课（MATH5开头的课程）平均75分以上，MATH7的课程至少修满4学分；发表（或者被接收）两篇学术论文，其中一篇是SCI，或者发表（或者被接收）一篇SCI一区或者二区的文章。
一般我每年只有招收一个博士生的名额（即使我有更多的名额我也精力有限，唯一例外是与其他导师联合招生，另一位导师同意做主要学业指导导师），通常硕转博发生在 春季学期开学初（可以是研一也可以是研二，要求已经通过资格考试，我更偏向于招研一转博），我会到时决定愿意跟我读博的学生中哪一位能用我的名额转博（如果明显无法入选的我会提前 暗示/明示劝退的，可以继续在我指导下完成两年硕士，也可以另找导师转博）。 作为我的研究生，你应该考虑在同时跟我读硕士而且有意向转博的学生之中你是不是最优秀的一个而且是否已经基本满足了我下文会提到的额外要求。如果拖到最后一刻无法在我这转博你才再去找其他的老师，对于你而言会变得很困难。
我大概描述一下我判断你是否“优秀”的标准。我会综合考虑以下几个方面。1，本科阶段已经学习过的内容，特别是和我的方向相关的，包括听课学习的和自己看书自学的。2，研究生基础课的学业成绩，和博士资格考试的代数成绩。3，自我认识你以来你进步的速度快慢。4，是不是积极主动学习。如何积极主动学习：读研究生一开始的时候你就应该不仅仅上课，还同时要关注学校里和国内甚至国外我们这个方向相关的学术报告和学术会议。你要自己主动去听报告，不一定是要听懂，首先得学习别人作报告的好的方式（学数学以后总要上台报告的），然后发现自己哪些名词完全没听过就要事后自己主动查资料补充一些这一方面的知识。一开始你可能一点都不了解究竟哪些报告是跟我们方向有关的，刚开始我会通过转发邮件或者微信告诉你哪些报告必须去参加、哪些报告建议你去听，在这个过程中你应该慢慢学会分辨哪些报告内容跟我们方向相关。渐渐地我不会总是提示你，过一段时间之后我就仅仅会给你转发个报告通知甚至不转发，你要自己主动去听报告。如果哪个报告我去听了觉得很好而我又没见你在场，那你会在我心目中减分。 科大本地的学术报告请注意学院主页的更新，如果错过了或者时间冲突还可以通过看视频了解（中科大网络课堂）。关于国内外会议、暑期学校等也一样，你要自己主动发现有哪些活动适合你参加：国内代数几何相关会议汇总，国际会议汇总：算术几何 数论 代数几何 。觉得适合的要主动去参加，一般会议会有资助年轻人的经费，我们学校也有支持参与交流的经费可以申请。同时你应该主动向我或者学院要经费资助去参加这样的交流活动，我在经费充足的情况下如果认为你想参加的活动适合你我将大力支持。如果你能在我告诉你之前发现一个确实适合你的活动并告诉我，那你就会在我心目中加分。如果某些活动包含有学生参与部分，你主动向会议方提出作小型报告那就很好。
由于代数数论和算术代数几何领域入门过程相对比较长，需要的预备知识相对比较多，所以让人看起来有一种高端大气上档次的感觉，其实到了做研究要创新的那一刻每个方向都一样的难。不要因为这是一个站在数学鄙视链顶端的方向而选择这个方向，年轻时小小的虚荣心可能会让你日后后悔当初的选择。我具体的研究方向在当前的数论与算术几何领域里算是相对比较具体和“简单”（较易入门）的方向，想了解更多信息，先去翻一翻我的论文的摘要和引言。
由于总的而言入门的基础知识储备需要非常多，我对招收博士生有额外的如下要求：
一开始进校时你愿意跟着我（或者科大其他代数方向的老师）读硕士，第一年跟两年毕业的硕士没太大区别，请参照上文。你要尽早表示希望跟我读博士，打算转博。我要求你就必须在研究生一年级已经通过了博士生资格考试（其中一门必选代数，另一门几何与分析任选 ，但我更希望你通过的是几何），所以从入学起 一共只有两次资格考试的机会（研一一开学和研一下学期开学不久）。同时要求研一的数学学分应该已经差不多达到博士毕业的学校要求（即专业课修过了32或者28学分，而且基础课平均必须75分以上，否则以后要分心应付考试无法专心科研 。如果你希望在研一下学期就转博，那就需要你上学期的基础课成绩特别优秀，表现出你也能轻松通过下学期的课程的本事。）。如果之前一直按照我的要求选课，那么研一结束研二开始这个时候你大概已经修过的课程应该有：代数学、交换代数、同调代数、代数几何引论、代数几何、代数数论等等，其中概型语言和代数数论的基本知识是最为核心的基础。 当若干个学生同时竞争转博名额的时候，你的代数数论和代数几何学得怎么样将会是我选择学生的最重要标准之一。
我指导博士的办法基本如下：研二开始 （或者更早，根据你的水平）会让你读一本我们方向的入门书，目前看来最好的选择似乎是Bjorn Poonen写的Rational
Points on Varieties与Colliot-Thélène和Skorobogatov的The
Brauer-Grothendieck group。半年/一年后我会让你开始读近期的论文，读完一两篇之后我会问你有没有可以提出来可做的问题，如果你能找到合理的问题那是最好的，如果不能我也会告诉你一个大概也许有希望可以做的问题。如果你顺利做出来写出文章那就差不多自然满足学校的毕业要求。但一般情况下不可能那么顺利，你不能只在一棵树上吊死，要在不断读文章的过程中去自己提出问题。注意：不要期望我源源不断给你提供可做的问题，读博士的过程要学会自己发现问题这个重要技能，我仅会在一开始的时候给你引导一个问题，以后要靠自己挖掘问题。我的博士导师也就差不多是这样指导我的，他最开始提的问题我没做出来，那个问题在我毕业后被同行做出来了。
也请注意，我不保证任何人能在我这毕业，读博有风险（题目永远做不出来自己又提不出别的问题、做到一半被别人新出来的结果全覆盖了、投稿若干次一直被拒。。。）请自行承担！关于发表论文，我个人更建议发表一篇好的论文就足以毕业，当然也不反对发表两篇论文毕业的方案，两者你自行选择，已经做出来结果之后我会给你建议。论文从投稿到被接收顺利的话要大约一年，如果中间被拒，重新开始算。。。论文从写好第一稿到拿去投稿要经历反复修改，特别是从无论文写作经历的博士生，这段时间需要大半年以上。我作为导师不会催你研究的进度，但你自己要对自己毕业的时间有个切实的期望和掌控（似乎还有规定最长不得超过8
年）。所谓博士论文导师，thesis
advisor，只会带你入门和给你写博士论文给指导性的意见和建议，论文归根结底是要你自己动脑子写。能否毕业拿学位归根结底也是你个人的事情。“能进大学就能毕业”这是最糟糕的假设，在我这里不成立，在任一所世界一流大学也不成立。
4. 直博生：
这似乎是2020入学的新增的，数学科学学院是科大的试点的学院之一。刚入学时我只能答应指导硕士，直到你的表现十分优秀并让我满意，我才会愿意收为博士生。如果你以直博生的身份进入科大，又想以后跟我读博士的话，那基本要求跟“3.
校内硕转博”是完全一样的。你入学后（甚至入学前，还在读大四的时候）就要尽早和我联系，如果我觉得你有机会以后成为我的博士生的话，我会指导你硕士期间的选课。行政手续上，一开始我不会同意挂名（研一并不是必须确定导师的，很可能会被挂在学院分管研究生的院长的名下
，如果必须要事先确定一个直博导师，那我无法答应：要么你放弃直博的名额从普通的硕士保送生读起，要么联系其他导师），直到按照上述要求通过博士资格考试后，在我的学生中竞争后成功转博，我才会正式接收。2020年10月加注：如果你希望跟我读研究生，当你收到直博名额的通知时请谨慎选择是否接受：我不愿意收直博生。
5. 从其他学校考博到科大读博士：
我基本上不收，特别优秀者例外。考前请先邮件联系，否则白考，我的招生要求比学校统一考试的要求高。特别优秀指：至少掌握了代数学、交换代数、同调代数、代数几何、代数数论的基本内容，懂概型语言。另外需要你的硕士导师以及另外至少两位老师
（最好是代数数论/代数几何方向的小同行，也可以是基础数学的大同行）书面推荐（由老师私下直接给我发电子邮件即可）。最好已经读过我的一些文章，而且能对文中某个问题提出见解。
J.-P. Serre : How to write mathematics badly.(渣画质，但这是Serre的报告而且是你能听懂的报告)
MIT的Poonen教授有这样的建议：Practical
suggestions for mathematical writing。
MIT的Henry Cohn教授有这样的建议。
怎样写一篇(学位)论文（梁永祺2021年5月）
1，姓名
2，推荐信的用途、截止日期、需要上传/发送的地址
3，学业成绩、排名等
4，我们大概什么时候认识，认识于什么场合
5，你有什么值得我写进推荐信里头的，也可以事先拟一个推荐信的草稿
当然我最后发出的推荐信肯定会和你拟的草稿不一样，我会加入我对你的评价（可能是正面的，但也不排除是负面的）等等相关信息。所以你要事先想清楚你自己是在我这留了个好的印象才好让我写推荐信（reference letter字面意思就是给出个人评价而不保证是正面评价）。
也请但凡有了申请结果也反馈一声，告诉帮你写推荐信的老师究竟你申请到想要的位置或资助没有，如果收到若干offer最后选择了哪一个。